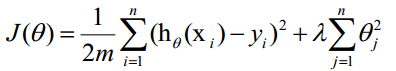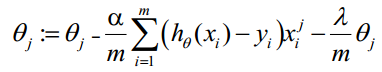data = pd.read_csv(‘路径’, header=None) #header=None可以解决pandas把某一行当成了列名的问题

line.strip().split(‘,‘)含义:
strip()用于移除字符串头尾指定的字符(默认为空格或换行符)或字符序列。 split(‘ ’): 通过指定分隔符对字符串进行切片,如果参数 num 有指定值,则分隔 num+1 个子字符串。
sigmoid定义代码:
是 Pandas 库中的一个函数,用于基于整数位置进行选取和索引数据。具体来说, 主要用于通过行号和列号来选取 Dataframe 中的数据。下面是一些常见的用法:
-
通过整数位置选取单个元素:
-
通过整数位置选取某行或某列:
-
通过整数位置选取多行或多列:
-
SSE(Sum of Squared Errors):
- SSE 是指每个样本到其所属簇中心的距离的平方和。对于一次聚类结果,SSE 越小表示数据点越接近它们所属的聚类中心,聚类效果越好。
- 确定最优K值的步骤:
- 计算不同K值的SSE
- 绘制SSE图
- 寻找“肘点”:在这张图表上,肘部法则的目标是找到SSE开始下降速率减缓的点。
- 选择肘点对应的K值:
-
轮廓系数(Silhouette Coefficient):
-
轮廓系数结合了聚类的内聚度和分离度,它衡量了每个样本与其自身簇内的紧密程度和与最近的其他簇的分离度。轮廓系数的取值范围在[-1, 1]之间,值越接近1表示聚类结果越合理。
-
确定最优K值的步骤:
- 计算不同K值的轮廓系数:
- a:样本与同一聚类中其他样本的平均距离。
- b:样本与最近邻聚类中的样本的平均距离。 轮廓系数计算公式为:

-
绘制轮廓系数图
-
选择轮廓系数最高的K值
-
-
CH指标(Calinski-Harabasz Index):
- CH 指标是通过计算簇内部的不相似度度量来评估聚类的性能。通过计算各类中心点与数据集中心点距离平方和来度量数据集的分离度,CH指标由分离度与紧密度的比值得到。CH index的数值越大越好。
原理——>特点——>原理详解——>核函数
- 原理和概念
- 基本思想是找到一个最佳的超平面,将不同类别的数据点分开,并且使得支持向量到超平面的距离尽可能远。
- 在二维空间中,超平面是一条直线,高维空间是平面。
- 非线性划分时,通常可以使用核函数和核技巧把这些点映射到高维空间里面解决
- 支持向量:指的是距离超平面最近的那些点,它决定了超平面的位置。
- 因为直线可以很多条,优化SVM是要找到泛化能力最强的超平面
- 泛化:经过训练集得到的模型在测试集或者生活中可以有很好的分类能力
- 数学模型原理,就是函数距离(下面)作为约束条件得到无数个能把样本正确分开的平面,然后通过目标函数在这些平面中找最宽的
- 特点
优点:
- 解决小样本的回归分类问题
- 核函数可以解决高维和非线性问题,同时不会增加计算难度
- 支持利用松弛变量可以允许一些点到分类平面的距离不满足要求,避免对学习有影响
缺点:
- 对于多分类问题不理想
- 难处理大规模数据
- 核函数需要多个尝试和调参
- 原理详解:

wT+b是能够判断出样本为+1还是-1类别的部分
函数距离:

就是样本类别乘wT+b。当正样本类别为+1,wT+b也为正;负样本类别为-1,wT+b为负,两种情况相乘结果都是大于0,距离只有大小没有方向。

中间为超平面,两边为支撑平面
我的理解是支持向量的点是距离超平面为1,然后其他点与之的距离就要大于1,然后建立初步模型

然后把模型转化为求最小值,同时也是转化为凸优化问题

然后利用拉格朗日乘子法(这个感觉不重要,而且也学过),将两个参数的优化问题转化为一个参数的优化问题,模型对应的KKT条件为: 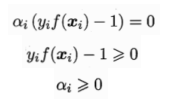
最后记住这个就好了
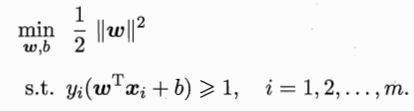
支持向量机的软间隔、核函数方法、支持向量回归都是在这个模型的基础上的
- 核函数
概述
非线性类型通常是二维平面不可分,为了使数据可分,需要通过一个函数将原始数据映射到高维空间,从而使得数据在高维空间很容易可分,需要通过一个函数将原始数据映射到高维空间,从而使得数据在高维空间很容易区分,这样就达到数据分类或回归的目的,而实现这一目标的函数称为核函数
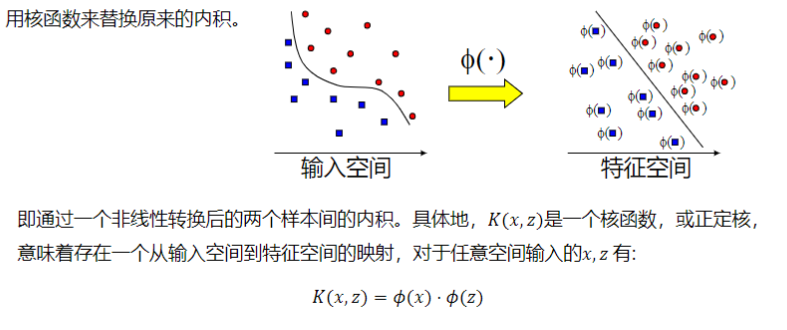
*线性SVM与核SVM的区别:假说集不同。*
*核函数的充分必要条件:**对称半正定矩阵。*



逻辑回归的原理——>优缺点——>常规步骤——>概率公式——>构造预测函数——>构造损失函数——>梯度下降法求解最小值——>向量化梯度下降——>正则化解决过拟合问题
- 原理:面对一个回归或者分类问题,建立代价函数,然后通过优化方法迭代求解出最优的模型参数,然后测试验证我们这个求解的模型的好坏。
- 特点:适合分类不适合回归,比较适合二分类
- 常规步骤:
- 寻找h函数(即预测函数)
- 构造J函数(损失函数)
- 想办法使得J函数最小并求得回归参数(θ)
- 概率公式:

解释:


函数h(x)的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为: P(y=1│x;θ)=h_θ (x) P(y=0│x;θ)=1-h_θ (x)
- 构造损失函数
损失函数是单个样本的,但是代价函数是对所有样本
cost和J函数都是基于最大似然估计建立的(使观测数据出现的概率最大化)

算法的代价函数是对m个样本的损失函数求和然后除以m:

- 梯度下降法求解最小值

-
向量化 梯度下降求损失函数最佳θ:
Vectorization后θ更新的步骤如下:

- 求 A=x*θ
- 求 E=g(A)-y
- 更新θ = θ - α * ∇θ J(θ)
-
正则化解决过拟合问题 解决方法 1)减少特征数量 • 可用人工选择要保留的特征; • 模型选择算法;
2)正则化方法 正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化项就越大。
正则项可以取不同的形式,在回归问题中取平方损失,就是参数的L2范数,也可以取L1范数。取平方损失时,模型的损失函数变为:
lambda是正则项系数: • 如果它的值很大,说明对模型的复杂度惩罚大,对拟合数据的损失惩罚小,这样它就不会过分拟合数据,在训练数据上的偏差较大,在未知数据上的方差较小,但是可能出现欠拟合的现象; • 如果它的值很小,说明比较注重对训练数据的拟合,在训练数据上的偏差会小,但是可能会导致过拟合。 正则化后的梯度下降算法θ的更新变为:
6. 梯度下降法代码实现
在这里的data数据集为这种

- 函数(梯度上升求最优参数):
- 每次迭代时使用整个数据集来计算梯度并更新权重。
- 计算所有样本的梯度后才一次性更新权重参数。
- 适用于数据量较小的情况。
- 函数(随机梯度上升):
- 每次迭代仅使用单个样本来计算梯度并更新权重。
- 使用随机样本来进行权重更新,减少了计算量。
- 适用于数据量较大的情况,能够加快收敛速度。
改进版随机梯度上升算法:
- 适用于大规模数据集
- 迭代过程中逐渐降低权重更新的幅度,使得模型在更新过程中更加稳定
凸函数——>三种优化问题——>正则化
- 凸函数
我的理解是转化为凸函数然后求极限得到最大值或最小值
- 三类优化问题
- 无约束优化问题:可直接对其求导,并使其为0
- 含等式约束的优化问题:拉格朗日乘数法将含等式越是的优化问题转换成为无约束优化问题求解
- 含不等式约束的优化问题:KKT条件(Karush-Kuhn-Tucker Condition)将其转化成无约束优化问题求解(支持向量?)
- 正则化(上面有提到)
关于考核中遇到的问题解决:
关于在训练模型时一开始我使用LinearSVC但是会报错’object has no attribute ‘support_’而使用SVM不会报错的问题,这个错误会出现在对于不支持稀疏矩阵的模型,就是比如这个LinearSVC,访问支持向量的属性。如果一定想要用,就需要加入参数的设置solver=“liblinear”。
到最大值或最小值
- 三类优化问题
- 无约束优化问题:可直接对其求导,并使其为0
- 含等式约束的优化问题:拉格朗日乘数法将含等式越是的优化问题转换成为无约束优化问题求解
- 含不等式约束的优化问题:KKT条件(Karush-Kuhn-Tucker Condition)将其转化成无约束优化问题求解(支持向量?)
- 正则化(上面有提到)
关于考核中遇到的问题解决: